In 1981, Daniel Kahneman, along with his long-time sidekick Amos Tversky, wrote a study about a very smart experiment they did that exposed the lack of attention people give base-rates in quick mental probability calculations. It is now quite famous, and you might come across it in a mathematics, economics or psychology course these days.
The Experiment
A cab was involved in a hit and run accident at night. Two cab companies, Green and Blue, operate in the city. You are given the following data:
- 85% of the cabs in the city are Green and 15% are Blue.
- A witness identified the cab as Blue. The court tested the reliability of the witness under the circumstances that existed on the night of the accident, and concluded that the witness correctly identified each one of the two colors 80% of the time and failed 20% of the time.
What is the probability that the cab involved in the accident was Blue rather than Green?
Have a think about how you would respond, given that you don’t have the time to sit there and work it out. What sort of percentage comes to you intuitively?
If you thought the likelihood of the cab being Blue was somewhere around 80%, you were in line with the most common responses. Unfortunately, however, you were also incorrect!
What the experiment showed was that the majority of people ignore the ‘base rate’, which is the ‘prior’ information or, if you like, sort of like the denominator of a fraction. People just tend to look at the ‘numerator’ part and consider that when making up their minds about likelihood. It’s almost like seeing a guy on the train with night vision goggles and then being asked ‘is that guy more likely to be an MI6 agent or an accountant?’. The circumstance makes the former answer seem more plausible in your mind, but you still have to consider that there are far more accountants than secret agents. Also, I don’t think a secret agent would be that conspicuous…
The correct answer is that the probability of the cab being Blue is 41%.
Doing the math
Getting the true answer is pretty difficult if you don’t have a pen and paper, as well as some familiarity with probability theory or a good sense of logic. But hopefully you will agree that if you had taken into account that 85% of the cabs were Green to begin with, this should reduce the value of any ‘Blue’ observations there have been.
If you do know probability theory, you will recognise this problem as a Bayesian one. You can use Bayes’ Rule and work out the answer pretty quickly. However, I don’t really like using formulae because they aren’t always logically transparent. I never really know whether I can trust the result, whereas if I’ve used logical steps and reasoning, I can check for plausibility along the way. This way, it’s easier to understand and also easier to explain to someone else. Hence, I’m going to show you how to get the answer above but by using a tree diagram to work out the conditional probabilities instead. It’s longer than plugging numbers into a formula, but it should make more sense.

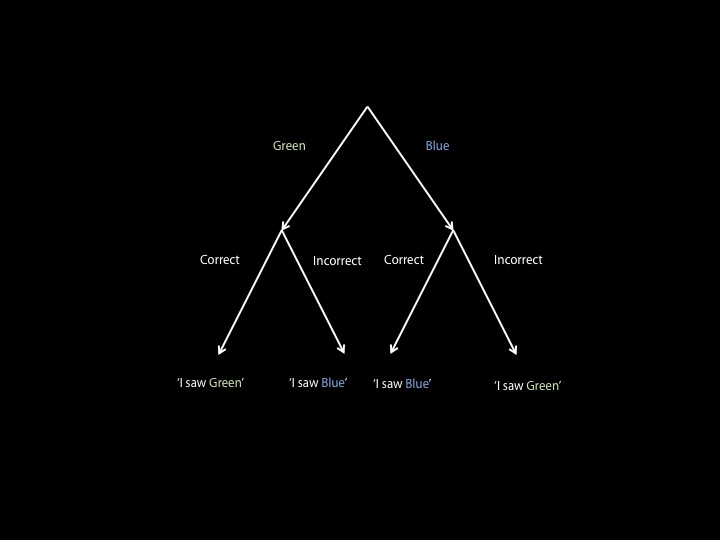
Let’s start with the cab in question. Obviously, the first bit of information tells us the cab is 85% likely to be Green (G) and 15% likely to be Blue (B), i.e. probabilities of 0.85 and 0.15 respectively.
Suppose the cab was G. This is the case 0.85 of the time. Now the witness can either be correct or incorrect about his observation, with probabilities 0.8 and 0.2 respectively. If he’s correct, he would have said ‘Green’ and if he was wrong, he would have said ‘Blue’. To get the probability of a sequence of events, you multiply them together. So he would say Green with probability 0.85 x 0.8 = 0.68, and Blue with 0.85 x 0.2 = 0.17.
We can repeat this same analysis for the case when the cab is actually Blue. All we do then is replace the 0.85 with 0.15 in our calculations. This might sound complicated, but the diagram below should help:

We can check that this is correct by making sure the probabilities at the ends of our branches all sum up to 1. This is because we have exhausted all possible cases that can occur. 0.68 + 0.17 + 0.12 + 0.03 = 1, so we’re all good.
Now we have to answer the actual question: given what we know, what is the probability that the cab was Blue?
Recall that the witness said he saw a Blue cab. This corresponds to our 2 inner branches. He could have seen a Blue cab and been correct, or he could have actually seen a Green cab and been wrong. So given that he said he saw a Blue cab, the ratio of it being Blue to Green is 0.12:0.17 or 12:17. Turning these into probabilities by summing them (29) and dividing by the sum, we have that the cab is actually Blue 12/29 of the time. 12/29 = 0.41379… which rounds to 41%, and we have the answer.
With this diagram, we can answer other questions about this scenario if we want to. As an example, suppose the witness said he saw Green instead. Now what is the probability the cab is Blue? Simple: the ratio is 3:68 so the probability of it being Blue is 3/71 = 4%. And here we see the power of the base rate. The initial proportion of taxis is vital in these calculations, but is easily overlooked when we’re making a quick judgement.

Surely this is faulty logic. There was one cab and it was either blue or green.
To bring the statistical nature of the numbers of green and blue cabs into the calculation is erroneous. Even on Kahneman’s theories, the cabs might have a bias as to where they are distributed (eg a major company might have a policy of only using blue cabs in their nearby location) – so who says that the cab had a statistical chance of being one colour against another. The cab was only one colour – the colour the supplier had it painted. To use the logic given in the ‘answer’ denies the statement that the witness was 85% right in assessing the colour of cabs, thereby undermining the whole analysis. There is a 15% chance that the cab was green.
“To bring the statistical nature of the numbers of green and blue cabs into the calculation is erroneous.”
This is what most people think (whether explicitly or implicitly), and is why they end up with the 80% blue answer.
“…so who says that the cab had a statistical chance of being one colour against another.”
Kahneman says it. Remember this is a hypothetical scenario. In real life, you also have these probabilities. The only difference is that here, all the information is taken into account and presented neatly to you. In reality, often, many of these base rates are implicit and unknown in precise terms. But you can still approximate them (that’s what actuaries and insurance people do).
Let’s rephrase the problem. Suppose I tell you I saw an alien in my house last night. All evidence points to the fact that I’m 99% truthful and correct in everything I say. Would you still think there’s 99% chance that I did see an alien?
Does the “All evidence” include any value judgement as to whether aliens exist and come to Earth?
Also, a one in a 900,000,000,000 chance can still occur and when single instances are being considered, needs to be taken into account.
This is a classic (and very clear!) example of Bayesian statistics.
The important thing to note is that prior information about a problem is a valid part of a (Bayesian) statistical argument. The fact that there are more green cars than blue *is* relevant.
The example you gave of a case in which there are 1,000,000 green cars if the perfect extension to the thought experiment. If there are 1,000,000 green cars and one blue and you are 80% reliable in your ability to differentiate them, then logically it is far more likely that you were wrong than that you saw that 1 in a million blue car. Bayesian statistics mathematically backs up this logic.
Explain how the stated premise of 80% accuracy of detecting the right colour is compatible with the statement that the taxi was blue (ie with 80% accuracy) is anything other than 80% accurate.
Work the logic back from the answer.
I was avoiding the use of formulae, but maybe it will help here. Let me call “Blue” the announcement by the witness and Blue (without quotes) the actual colour of the cab.
The question is asking us to work out the probability of the cab being Blue, given that the guy said “Blue”. In other words we want to know P(Blue|”Blue”). However, this is not the same as P(“Blue”|Blue) which is the probability that the guy says “Blue” when the cab actually is Blue. This is where the error comes in.
P(“Blue”|Blue) = 0.8, this we are told. But I believe you are saying P(Blue|”Blue”) = 0.8 too, which is not correct.
Bayes’ rule tells us:
P(Blue|”Blue”) = [P(“Blue”|Blue) * P(Blue)] / P(“Blue”)
P(Blue|”Blue”) = [0.8 * 0.15] / 0.29 = 0.41… = 41%
I’m afraid that’s about as clear as I can be, though I think the article explains it in a more intuitive way.
That’s not answering the question.
Given that “Blue” is the answer given to 80% accuracy according to the court’s tests, (taking the 80% stated as being a premise), then work back to Blue/Green probablilities.
Call the process by whatever name you like it oughtn’t to alter the mathematical process.
What was the decision on the “all evidence” actually being somewhat less than that used to come up with the “answer”?
Simon I am an alien.
You are observing this. The chance of you reading this correctly is very high but not 100%.
Is it more likely you are misreading this and I am not an alien, or you are reading this correctly and you have made contact with another world.
To state the obvious, ignore the fact I may be lying, this is irrelevant for this example. If you don’t understand this, it is because my alien brain ray is confusing you.
PS I am not an alien, I am a llama.
Your whole reply is irrelevant
Sorry, the text had scrolled up out of sight and I didn’t go back and check exchange 20% for 15%!
If there were 1,000,000 taxis in the city all green except for one blue one and a witness who in good daylight could tell the difference between blue and green with 100% accuracy (but in heavy rain, poor light and seeing a fast-moving taxi was only 99.9% accurate)said it was the blue one, would there still be a chance of the taxi actually being green?
However, the fact remains that to include the proportion of the different coloured taxis in the calculation makes a nonsense of the basic premise that the witness could tell the colour to 80% accuracy – thereby making a nonsense of the whole calculation.
In the case of a court, an assessment of the global odds regarding the event (the witness is only right 41% of the time) would be fallacious and a travesty of justice. Once the witness has made his claim, it is his reliability alone that is at question.
To wit, there are 1,000,000 cars in my city of which 100,000 are black, 100,000 white, etc distributed evenly over ten different colours. I correctly identify car colours 90% of the time. By this Bayesian principle if you ask me “what colour was that car” I will be correct precisely 50% of the time for any given colour.
A person who identifies car colours correctly 90% of the time will thus identify car colours accurately 50% of the time. This is not possible. Ah, perhaps, you say, he is really only right 50% of the time, in which case he is NOT right 90% of the time. If, however, we adjust my accuracy down, the Bayesian figures will also drop, etc. forever. Thus, by this principle, people’s accuracy is always lower than their accuracy–an absurdity…if, that is, you are asking me the concrete question “what colour was that car.”
To make it yet more clear… I won’t type out all the numbers, but going on a 1/13 million, the chances of a person who reads a string of 6 numbers correctly 99.9 percent of the time concluding accurately that he has won the lottery after one reading of his ticket is .05% or so.
In both situations, the Bayesian principles hold up with regard to the event taken globally, but they do NOT hold up as relevant to a court’s project of identifying what really happened in a particular instance. Over the course of a million people with 99.9% accuracy reading numbers, only .05% of them will ever correctly conclude that they have won the lottery in large part because most of them will never think they did. Of those that DO think they did, 99.9% of THEM will be correct on the first reading. Thus, the question of whether a specific claim to winning the lottery is correct is a question exclusively of the witness’ reliability, and ditto with the cabs, and me looking at cars.
If a court were to fail to recognize this, it would, ironically, be committing a form of the gambler’s fallacy. The global odds of all witnesses of this accuracy being right about all incidents is irrelevant in precisely the same way that having rolled a 6 one time has absolutely no influence on whether I will roll one again, even though the global odds of two 6s is much smaller than the odds of one.
Aliens are a complete red herring since we do not even have confirmation that they exist, and certainly cannot calculate the odds that you really saw one.
Dan: in your example of being 90% accurate and there being ten different equally likely colors of car, the witness *will*, in fact, be 90% correct — not 50% correct — when he says “black”. Let me walk you through it. Is it okay if I revise it to 91% correct, by the way? That way he can be 91% right, and 1% likely to choose each of nine wrong colors. Adds to 100%. Avoids messy fractions.
Suppose he says “black”. He would do that for 91,000 of the 100,000 black cars. He would do that for 1,000 each of the white, yellow, green, baby blue, turquoise, etc cars… leading to 9,000 wrong calls of “black” versus 91,000 right calls of “black”. 91% accuracy.
This doesn’t even depend on him being equally like to make any mistake. Suppose that for some reason, he’s 91% accurate, but — and the court doesn’t realize this — he will always guess “plaid” when he’s mistaken (and there aren’t any plaid cars). Well, in that case, *if* he says “plaid”, he’s 0% accurate. This happens 9,000 times for each color of car (90,000 total). But he also gives 91,000 accurate answers for each color of car (910,000 total). He’s still 91% accurate overall.
Sorry, one more way to make this SUPER clear. Look at the diagram above. 2 of the 4 final options are people saying “I saw Green.” Those have been absolutely ruled out by the time the witness says “I saw blue.” There is a precisely 0% NOT 68% chance of the witness correctly saying “I saw Green” and a precisely 0% NOT 3% chance of the witness wrongly saying the same. Thus, the only relevant data are in the two middle results and it is the odds of accuracy and those odds alone that are now at play. 80%.
Right…that made it less clear and was wrong. Back to post 1….
Alright, I’m ready to wholly reverse my position, with a crucial note about why this is so counter-intuitive. First, a scenario:
There is a rash of hit-and-run accidents in town. There have been 100 in a row. In reality, they are evenly distributed between cabs. 85 were green, 15 were blue. John has witnessed every single accident, and is the only witness. Every victim is dead. Conditions were identical for John’s vision. In each case we interview John and apply Bayesian statistics to decide whether to arrest a green cabby or blue cabby. Because the incidents are isolated, we do not commit the gambler’s fallacy, and run the numbers individually every time. Every time we conclude that John is probably wrong when he says he saw blue, and very probably right when he says he saw green. We arrest 100 green cabbies, and 0 blue cabbies. We will be right 85% of the time. If we had listened to John we would only be right 80% of the time. For us, there will be 15 wrongfully arrest green cabbies and 0 wrongfully arrest blue cabbies. If we had listened to John there would be 17 wrongfully arrest green cabbies and 3 wrongfully arrested blue cabbies. In cases where John says “green” our wrongful arrest rate will be 5%. In cases where he says “blue” it will be a wopping 41%. But that all adds up to a net 15% since the cabs are not evenly distributed.
So, the numbers check out over time. Disbelieving John does result in a somewhat better outcome.
Regarding my own Lottery example, my flaw here is most likely that people A) Never really read a winning ticket only once, B) Are probably MUCH more accurate than 99.9% especially if they read a ticket twice. If my friend is, in fact, a more plausible 99.99999999999% accurate after two readings, the numbers start to be sensible. 99.9% seems extremely accurate, but for this kind of operation it is probably a pitiful guess of human accuracy if the person is really trying (and he would be if he thinks he won the lottery).
So, why is this all so counter-intuitive? I think for two reasons. First, the accuracy numbers. An 80% accuracy in colour ID for John is incredibly awful. Normal colour ID for an adult would be vastly larger, probably well about 99%. John’s low accuracy rate would mean he was in almost total darkness with rain, or colour-blind, not wearing his glasses etc. If we made John’s conditions more concrete in the problem, a reader might be much more willing to believe that Bayesian principles. “John’s accuracy in the near blackness with rain is only 80%–how likely is it that the car was really blue?” Just flatly saying 80% does not register with our real experience easily. We don’t have an intuitive sense of what that means.
Second, the wrongful arrest rate of 41% is ungodly terrible too, and the fact is that we virtually never deal with real-life situations in which we really have absolutely nothing more to go on than John’s eyesight in terrible conditions. We can’t actually accept a certainty rate of 80% for John because we can’t REALLY imagine not having more info like John noticing other things about the situation, the victim seeing the cab too, or the bad visibility conditions being explicit.
If a real jury really did have this little evidence to go on, they should acquit, and almost certainly would. The puzzle is misleading because of its tremendous distance from real life.
Also, an 80% color identification rate is NOT awful. It’s quite good.
Here’s the thing: human memory is not a camera. An adult with good sight could probably identify color better than 80% accuracy *while looking at* the event. But that’s very rarely how police witnessing goes. Normally, time has passed; normally, the witness had other things to concentrate on while the event was occurring; normally, most of the event has already happened by the time the witness realizes “Oh hey, this might be significant”. And there’s no telling, then, which details they’ll try to process, or what mental framework they’ll use.
Intro to psychology classes frequently find an opportunity to stage a sudden, unannounced intrusion and kerfuffle during a class, in order to have the students write afterwards about what happened. The accuracy of the details written will average far, far lower than 80%.
By the way, aliens are still irrelevant. 😉
Sorry, I don’t get it. The probability of it being blue is the middle 2: 29%. 41% is the probability of it being blue AND the witness being right about it. What have I missed?
This is what I thought too when I first tried solving it, which is why I am here. I’ve realized that the wording of the problem is a little tricky. The final question does indeed ask the probability that the cab involved was blue rather than green and that would indeed be 29% without the statement “given the witness says he saw blue” which was mentioned in the second bullet point of the problem. So it is implied that the witnesses us identified it as blue so of the 29% of the times that it is blue and the witness correctly identifies it as blue, which happens 12% of the time since .8*.15=0.12, then the probability that it is blue and correctly identified is just 12/29. It’s easier to think about if you look at a sample of 100 cars. 85 are green, 15 are blue. Of the 15, 12 are correctly identified and of the 85, 17 are incorrectly identified as green and are thus blue. Of those 29, only 12 were correctly identified which is 41% of 29.
When a blue cab goes by you see it correctly 80% of the time. When a green cab goes by you see it incorrectly 20% of the time. Given green cabs out number blue cabs 85 to 15. Out of every 100 cabs passing by You will see 17 green cabs as blue (20% of 85) and you will see 12 blues cabs correctly as blue (80% of 15). So out of every 100 cabs passing by your chance of seeing a blue cab correctly is 12 out of the total (12+17) = 29 blue cabs you ‘saw’ or 41%. I can’t say it any simpler than this. Hope this helps those questioning the logic. You have to consider that you are more likely to see a green cab because there’s more of them even though you think it’s blue.!
One other way to think about it … Say that the witness can correctly identify the color 80% of the time but we happen to know thay there were ONLY green cabs and NO blue cabs out that night … What are the chances now that the witness was right?
Neel – thank you for explaining this! Very much appreciated. I was looking for a non-mathematician explanation, and you provided it … thereby saving my brain from melting.
The man is 40 and marries a girl 10 years old. That means the man is 4 times the girl’s age.
5 years later the man is 45 years old and the girl is 15 years old. This means that the man is now only 3 times the girl’s age.
15 years later the man is 60 years old and the girl is 30 years old.
This means the man is now only twice the girl’s age.
How many years will it take until they are both the same age?
See my point?
If hour witness saw a blue a cab, he saw a blue a blue cab. As a Law student I would like to see that one fly (discrediting the witness) in court. 80% is 80%.
However, reasonable doubt is almost absolute certainty. 80% is not almost absolute certainty. Almost absolute certainty would be 99.9%. Either the Crown loses.
I read this study before in Statistics class. But the real test is, can the witness tell the difference between Green and Blue, as both colours are close, unlike black and white. Out of 85 green cars the witness correctly identified 80% correctly. When the witness saw 15 blue cars he was correct 80% of the time. 80% is 80%. You cannot combine the studies. If you are a student in school and you write your English exam to which has 85 questions and you get 68 questions answered correctly your teacher scores your exam at 80%. Now you take the Math test. There are 15 questions. You answer 12 questions correctly. Again your teacher scores your exam at 80%. The Dean will score your final grade at 80%.
In our case, the court tested the witnesses ability to tell the difference between Green and Blue. He did that with 80% accuracy. You could pass 500 cars in front of the witness. At then end of the day, how many did he get correctly? That is it.
But again the Court would not accept an 80% score. That is reasonable doubt for a criminal trial. However, if this is a civil case, personal injury law-suit all Plaintiff has to prove is beyond probabilty which is 51%. The witness testimony would stand.