How many games are there in a tournament?

In keeping with the football spirit, I’m going to use the format of the FIFA World Cup as an example to show you how to calculate the total number of matches/games played in a tournament.

There are two cases that we need to consider:
1. The league stage – where every team plays every other team in a group
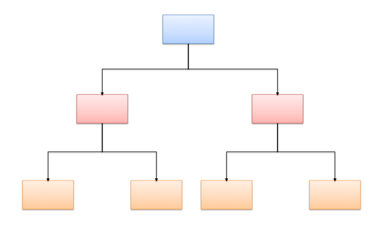
2. The knockout stage, which follows a structure like that shown in the picture above, until one team is declared the winner

I’ll derive a general formula for each stage that you can then apply to any tournament situation involving a league, a knockout, or both.

The League Stage

I’m sure you all know the format of a league, but I’ll define it explicitly anyway.

• You have a bunch of n teams (or individuals, or anything else that you want to pit against one another).
• Each team plays every other team once.

Some of you may have noticed that the structure of this problem is the same as the famous ‘handshake problem’. This is where there are n individuals at a party and they all must shake every other person’s hand. The problem is to work out how many handshakes there must be in total. If you don’t already know the answer, you might want to stop and think about how you might go about working this out before you read on.

Let’s consider some simple examples first. We will call our teams A, B, C… for simplicity.

Suppose there are 2 teams (so n=2) in our league table. Obviously, in this case, there can only be one match:

A vs B

What about when n=3? We now have:

A vs B B vs C
A vs C

So there are 2+1 = 3 matches in total. Note that I have put the matches into 2 different columns. I’ve put all of A’s matches in the first column and all of B’s in the second (that aren’t already in the first column). There’s a reason for this which will become clear in a moment.

For n=4 (the number of teams in each world cup group):

A vs B B vs C C vs D
A vs C B vs D
A vs D

So now there are 3+2+1 = 6 matches.

Clearly there’s a pattern forming. The total number of matches is given by:

1 + 2 + 3 +… + (n-2) + (n-1)

This gives us the answer, but it is quite cumbersome to calculate all of this when n becomes large. If there were 100 teams, it would take quite a while to work out 1 + 2 + 3… + 98 + 99. Luckily, there’s a formula that we can work out to make our lives a lot easier.

Look again at the pattern of matches that I wrote out for n=2,3,4. To make it simpler, lets just denote each match with a * and count the *’s:

n=2:
*

n=3:
* *
*

n=4:
* * *
* *
*

Hopefully, you can see that for n=5:
* * * *
* * *
* *
*

We seem to be getting nice neat triangles (which is why the totals are known in mathematics as ‘triangle numbers’). We all know how to find the total number of items in a grid: just multiply the number of rows by columns. Well, we can turn the above diagrams into nice grids by duplicating the diagram, turning it upside down and sticking it onto the end:

n=3:
* * *
* * *

n=4:
* * * *
* * * *
* * * *

n=5:
* * * * *
* * * * *
* * * * *
* * * * *

Now these grid totals are easy peasy to work out by multiplying the number of rows by number of columns:
• n=3: 3 x 2 = 6
• n=4: 4 x 3 = 12
• n=5: 5 x 4 = 20
• n=n: n x (n-1) = n(n-1)

Finally, since we want to work out only the number of white stars, we just halve our totals. This gives us the overall formula:

Number of matches in a league = 0.5n(n-1)

Of course, if we are in a league where every team plays each other twice, we can just multiply this number by 2. If they play each other 3 times then we can multiply by 3, and so on.

The Knockout Stage

Now we come to the second tournament format – the knockout stage. In this format, n teams are paired up in matches. The winners are then paired up in a second round of matches. This carries on until there is a final match between 2 teams, the result of which determines the winner of the tournament.

The total number of teams in a knockout competition must be a power of 2. This is because we are halving the number of teams at each stage, and the only way we can keep halving n until we get to 1 is if n is a power of 2.

For n=2, there is only one match and one round.

For n=4, there is a semi final round where there are 2 matches and a final where there is one match. Hence there are 3 matches in total (this is the example in the diagram at the top of the page).

For n=8, there are 4 matches in the first round, 2 in the second and 1 in the third. The total is 4+2+1 = 7.

Again, there is a pattern forming. In the previous case, there are 8/2 = 4 matches in the first round, 8/4 = 2 in the second and 8/8 = 1 in the final round.

So in general, we can say that:

• 1st round = n/2 matches
• 2nd round = n/4 matches
• 3rd round = n/8 matches
• Eventually, the final round has n/n = 1 match

Our formula is:

Total matches in a knockout tournament = S = n/2 + n/4 +… + n/n

(I’ve called the total S to make it easier to work with)

Like the league stage, we can simplify this into a neat formula using some clever maths.

First, we halve the entire sum so that:

S/2 = n/4 + n/8 +… + n/2n

Subtract this from our original S equation:

S – S/2 = n/2 + (n/4 – n/4) + (n/8 – n/8) +… – n/2n

You can see that most of the terms cancel each other out. The only ones that don’t are the first and last ones. Also, S – S/2 is just S/2, so:

S/2 = n/2 – n/2n

But n/2n is just 1/2 since we can cancel out the n from the numerator and denominator:

S/2 = n/2 – 1/2

Finally, we multiply both sides of the equation by 2 to get the overall formula:

Total matches in a knockout tournament = S = n – 1

Isn’t maths lovely? All of that complicatedness turns into a stupidly easy formula! Just subtract the number of teams by 1 to get the total number of matches in a knockout tournament.

Number of matches in the world cup

Let’s apply these 2 formulae to the world cup.

In the group stage of the world cup, there are 8 groups consisting of 4 teams each. Each of the groups is a mini league where each team plays each other team once. Using our first formula when n=4, we have 0.5 x 4 x (4-1) = 0.5 x 12 = 6 matches per group. Therefore, we will have 6 x 8 = 48 matches overall in the group stage of the world cup.

In the knockout stage, we have 16 teams, so there will be 16 – 1 = 15 matches in total.

This gives us 48 + 15 = 63 matches overall in the world cup. Or so it should be, but sneakily, the world cup has a third place playoff match added on to the end. So there are 64 matches in total.

These formulae have far more applications than just calculating matches in a tournament. Maybe you’ll be able to spot similar patterns in other situations and apply one of these formulae. That’s where the real magic of mathematics comes alive.