Mathematic Logic for Beginners

When my friend stated that he’d like to learn a little more maths to help him with programming, I saw it as an opportunity to write a little about mathematical logic operators. I don’t know how helpful it will be for him specifically, but hey, it’s fun to write about!

If

The logical operator that forms the basis of most logical statements is ‘if’. It’s a way for you to make a claim, and is usually used in conjunction with the word ‘then’ to make an assertion given an assumption.

For example:

1. If my face is made of lead, then I am the King of Spain.
2. If it is raining, then my feet will get wet.
3. If the lamp is switched on, then turn off the microwave.

The general form of the statements above is “If A, then B”. The A part states some condition that needs to be satisfied in order to proceed with the rest of the statement. If the A part is not satisfied, then we can’t say anything more about the B portion of the statement. This is quite an important point! It does seem to trip some people up in more complicated statements.

The first statement emphasises this point. You might be tempted to look at that and think “This statement is wrong! You would never be the King of Spain!”. Whilst you may look at my peasant-like apparel and make the valid observation that I am not the King of Spain and am unlikely to be, you cannot possibly state that the statement is false. To do so, you’d have to see that my face is made of lead first and then show that I’m still not the King of Spain. But since there is no way of doing so, this rather silly statement is still technically a correct one!

Let’s look at the second example. The thing we have to check is whether it is raining or not. If it is, then the A portion of the statement is satisfied. So we move on to part B, which tells us that my feet will get wet.

Note that this is an assertion that hasn’t been proven to be true or false. To do so, we have to check that given A has been satisfied, we can observe that B is also satisfied. In other words, if it is raining and I see that my feet are wet, the statement holds in that case. However, if it is raining and my feet do not get wet, then we have shown that A is satisfied, but NOT B. In that case, we have ‘negated’ the statement.

The final statement is more of an instruction than an assertion. It tells you that when you see A has been done (the lamp has been turned on) then B should be done in response (the microwave should be turned off). These are the kinds of ‘if’ statements that you see more commonly in programming, because you are telling the computer to execute some instruction given a condition that you have imposed on it. A type of statement that is often used checks whether a variable is of a certain value and then returns some output:

if (x == “Male”)

return “Sorry, this program is only designed for females.”

else…

This is some pseudocode (it’s not written in a real programming language but is a kind of ‘sketch’ of what a chunk of code is supposed to look like or do) for a small procedure that looks at the variable x and checks to see whether it is equal to the string “Male”. If it is, then the program will display a message telling you that you can’t use it. If not, then it will continue with whatever else the program does.

Boolean Operators

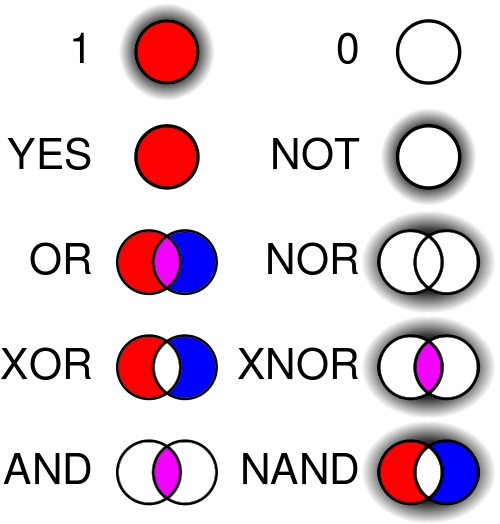
In logic and computing ‘Boolean’ values are things that can only have 2 possible states: True (or 1) and False (or 0). The reason for their common usage in programming is derived from the fact that electrical signals can either be on or off (and is the reason for everything else binary in the computing world). The image at the top of this page sums up these operators quite nicely. I won’t go through them all but I’ll give you a few examples of the kinds of things they are used for.

1. If it is below 20°C and the heating is off then switch the heating on.
2. If my hand is broken or my foot is broken then go to the hospital.
3. If the car is dirty or the seats do not smell lemony fresh nor does the leather sparkle, then clean the car.

The first requires that both conditions be satisfied before the heating is switched on. The heating wouldn’t turn on if the heating was off but the temperature was 30°C, for example.

The second requires either condition (or both) to be satisfied. It only takes one broken limb, thankfully, to send me to the hospital. If I wanted to be convoluted, I could make that into an XOR statement. This is the same as using OR, but it means that the conditions have to be ‘exclusive’. In other words, if both my hand and foot were broken then it wouldn’t send me to the hospital, but it would if just one were broken!

The final one is mostly there to demonstrate that you can go crazy with inserting operators in between operators ad infinitum. But as far as programming philosophy goes, it’s important that you don’t get completely carried away! Although the computer can understand it, you might struggle to, and that is less than useful if something goes wrong.