The best way to remember things, at least I find, is by association. If something reminds you of something else and you can make the mental chain that links them together when you come across something, you can easily recall what you need to. I’m sure those guys that can memorise decks of cards will tell you the same thing.
Something that comes up a lot in economics, maths and anything else that involves some form of logical statement is the distinction between conditions that are necessary but not sufficient; sufficient but not necessary; or both necessary and sufficient for something to be true. It’s perhaps not difficult to figure out what they mean just by the language they use, but I find that I still have to ‘decipher’ what they mean in any particular context rather than just intuitively understanding. By accident, when I was thinking of something else, I thought of a nice analogy I can think of in terms of friends/relationships that helps to ‘visualise’ these conditions. Hopefully they might help you too…
Sufficient but not necessary
You walk into a bar and have a chat with a stranger. They seem kinda nice. They keep you occupied for the evening (and maybe the night…), but you then part ways and get on with your life. Or you have lunch with a work colleague and have a decent conversation before returning to work again. These people are sufficient in that they keep you happy and occupied, but they are not necessary. You can live without them pretty easily.
Sufficient but not necessary, then, pertains to those situations where if the condition is met, then everything works out. But there may be other conditions that will also do the job. A mathematical example might be the following:
Take the quadratic (x-4)(x+4)=0. If I said “(x-4)(x+4)=0 has a unique solution for x>0”, then this statement would be sufficient but not necessary. Why? Well it’s enough – x>0 means that the only solution would be x=4. But it’s not necessary, because, for example, the equation also has a unique solution for x<0, which is -4. x>0 keeps you pleased, but x<0 will do the job too.
Necessary but not sufficient
This is your close friends, your best friend, maybe your sibling or parents. They are people you need but they are not enough for you on their own. You may have a best friend who loves partying and takes you out places, which you appreciate. But being around them all the time might be draining, and so you might also need someone who was a little quieter too.
This is the idea behind necessity. Mathematically, have a look at this function:

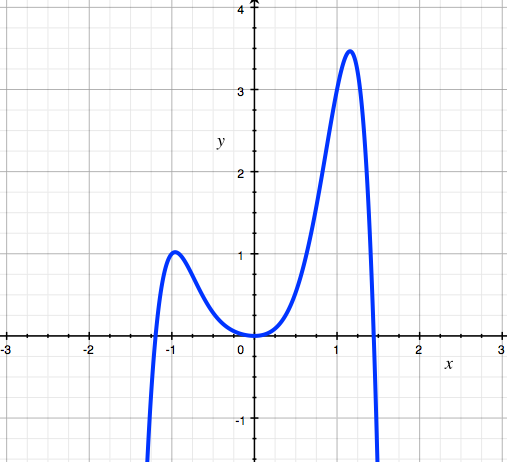
This is the graph of y=-2x6+3x4+x3+x2 . If I wanted to find the maximum of this function, I’d take the first derivative dy/dx = 0. But this is a necessary condition and not sufficient. Why? Setting the first derivative to 0 gives us the stationary points i.e. where the graph is flat. As you can see, there are 2 of these flat points (the peaks of the humps), but only one of them is a maximum. So you do need dy/dx = 0 to find the maximum, but it’s not enough on its own.
Necessary and sufficient
This is the ‘one’, the soul-mate. Whether you’ve seen enough Meg Ryan and Tom Hanks films to believe that such a thing actually exists, imagine there is someone who you can’t live without. In addition, you would be perfectly happy to be stuck alone with them for the rest of your life on a desert island. They tick all the boxes – they are your best friend and meet all your various different requirements for a social companion. Congratulations, you have just found someone both necessary and sufficient. Now go away. I don’t need your smugness, thank you.
There are many things you can think of I’m sure that depend on only one condition to be true. If you were looking at a polynomial like the one above, a sufficient and necessary condition that the polynomial has at least one real root is if it crosses the x-axis. This sort of comes out of the definition of a real root really, but crossing the axis is still a sufficient and necessary condition, because if you can see that then you know the root exists, and importantly, that’s all you need to be able to see.
Forget the mathematical examples if you don’t need them, I think the important thing to keep in mind is a little story, like my idea about friends. You may have a better one, but being able to link these conditions to something you naturally think about should help you both understand and remember them better.