My favourite bits of maths are related to pure number theory. It’s the stuff that we owe the Ancient Greeks a whole lot to. A lot of the things they came up with form the cornerstone of mathematical theory today.
The Greeks were obsessed with the beauty of numbers. They liked everything to work out nice and neat, and this meant that their proofs and theorems were very elegant on the outside (though they incorporated a lot of imaginative and abstract thinking behind the scenes).
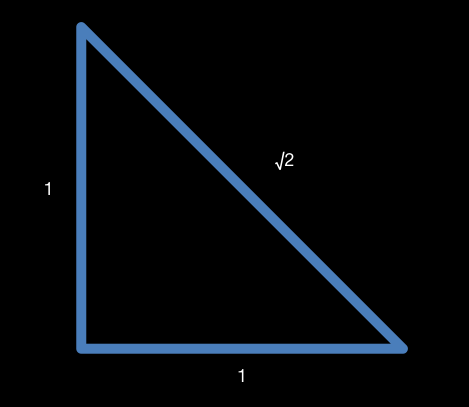
Unfortunately, this meant that they got a little irritated when things didn’t work out so nicely. One such instance came down to Pythagoras when, after championing his theorem about the sides of a right-angled triangle, he came across a problem in trying to work out the length of the hypotenuse when the other two sides were of length 1. That problem was √2. ‘Haha’, I thought, when I first heard that story many years ago. ‘Stupid Pythagoras’. Yet, the puzzle was not an easy one to solve.
Of course, you probably know that √2 is an irrational number, because this would have been something that you were told. This means that you cannot express it as a nice fraction, and, as a result, writing it out as a decimal number is also futile because it will go on forever.
However, to actually show that it is impossible to write out √2 explicitly is easier said than done. When I thought of it as being a nice proof to look at, it turned out to be a lot more difficult to crack than I expected! The proof emphasises the beauty of number theory, and will hopefully also make the point that there’s a lot more going on behind the things we take for granted than it may seem.
The Hard Bit
There is a preliminary proof that I need to do in order to prove that √2 is irrational. I’ll try to take this slow, because conceptually, it is not so easy.
I need to show that:
For any positive integers p and q, we have that p2 ≠ 2q2
Eh? ‘Why should this be the case?’ you say. Good question. It’s not obvious, which is why we want to prove it. Try putting in some numbers for p. 32 = 9 but 9/2 = 4.5 which we cannot obtain by squaring a number. 42 = 16, 16/2 = 8 and 8 is not a square number either. Try this with more numbers if you want. Eventually, you might resign yourself to the fact that it probably cannot be done.
To prove this, we are going to assume that it is true first of all. In other words:
Suppose p2 = 2q2 for some positive integers p and q
If this is true, then it means that p2 is even (because it is a multiple of 2). But if p2 is even, then it means that p must also be even. It is quite easy to prove that squaring an odd number will always give you an odd number, so I won’t do this here (although if anyone is having trouble with this then leave a comment).
Let’s call the smallest value of p such that the above relationship is satisfied P. So, for this P, we have that:
P2 = 2Q2
for some positive integer Q.
P is even, as we know that all values of p are even. Therefore, since even numbers are just multiples of 2, we can write:
P = 2M
for some positive integer M.
Now we can substitute in for P in the original expression, so that:
(2M)2 = 2Q2
4M2 = 2Q2
2M2 = Q2
Can you see what this tells us about Q? Well, Q2 is a multiple of 2, so Q2 must be even. And from what I said before, if Q2 is even, then Q must also be even. So, just like we did with P, we can write Q in terms of some positive integer N:
Q = 2N
Now, we can substitute that into the previous expression involving M and Q:
2M2 = (2N)2
2M2 = 4N2
M2 = 2N2
Want to guess what’s coming next? M2 is a multiple of 2, so M2 is even, and therefore M is also even! Does this expression look familiar? The relationship between M and N is exactly the same as the relationship between P and Q.
This means that M is another possible value for p. But what is M? Let’s look back up our equations. We defined M such that P = 2M. Hence:
P > M
Uh oh! We have a contradiction! We defined P as the smallest possible value of p. But M is also a possible value of p, and M is smaller than P. So P cannot be the smallest possible value of p!
If we use this argument recursively, it will go on forever. This means that there is no smallest value of p because we can always find one smaller. But if you have a set of numbers, there has to be a smallest one… unless the set is empty! Therefore, we have just shown that the set of numbers that satisfies p2 = 2q2 is empty. In other words, this relationship is impossible to satisfy!
The Easy Bit
That was probably a bit difficult to get your head around (if not, then you should take up mathematics at a high level if you aren’t doing so already!). Now, we can prove that √2 is irrational, and this is actually quite easy in comparison.
A rational number is one we can write as a fraction p/q for some integers p and q. Of course, since √2 is positive, p and q must also be positive. So what we want to prove is that:
There exist no positive integers p and q such that √2 = p/q
As we did with the previous proof, the way to approach this is by contradiction.
Suppose there exist some positive integers p and q such that √2 = p/q
Squaring both sides gives us:
2 = (p/q)2
2 = p2/q2
2q2 = p2
Aha! We have proved earlier that there cannot exist positive integers p and q such that this equality is satisfied. Therefore we have a contradiction. Hence, our assertion that √2 = p/q must be false. Of course, this means that √2 is not a rational number. Thus, √2 is an irrational number!
And with that, we’ve opened up a whole new realm of numbers – ones that we need to use but that we can’t write out explicitly. Isn’t maths exciting?